티스토리 뷰
📌DFS
Depth-First-Search
깊이 우선 탐색이라고 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘
📌그래프 표현 방식
1. 인접 행렬: 2차원 배열로 그래프의 연결 관계를 표현하는 방식
2. 인접 리스트: 리스트로 그래프의 연결 관계를 표현하는 방식

위 그래프를 각 방식으로 표현한다면 다음과 같다
📌인접 행렬 방식

2차원 배열에 각 노드가 연결된 형태를 기록하는 방식
파이썬에서는 배열을 리스트 자료형으로 표현할 수 있으므로 인접행렬을 리스트로 구현함
INF = 99999999 # 무한의 비용 선언
# 2차원 리스트를 이용해 인접 행렬 표현
graph = [
[0, 7, 5],
[7, 0, INF],
[5, INF, 0]
]
print(graph)
연결되어 있지 않은 노드끼리는 무한의 비용(INF)이라고 작성함
📌인접 리스트 방식
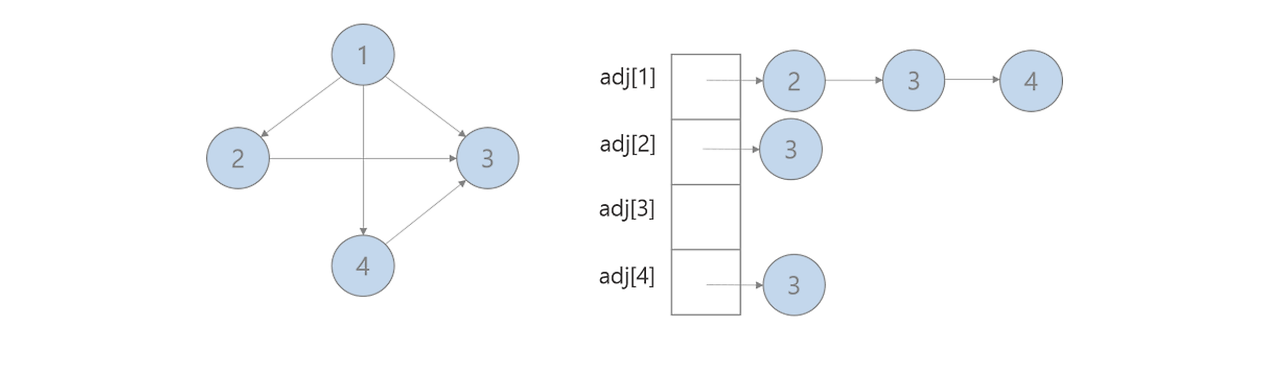
모든 노드에 연결된 노드에 대한 정보를 차례대로 연결하여 저장
파이썬은 기본 자료형인 리스트 자료형이 배열과 연결 리스트의 기능을 모두 기본으로 제공
파이썬으로 인접 리스트를 이용해 그래프를 표현하고자 할 때에도 단순히 2차원 리스트를 이용
# 행이 3개인 2차원 리스트로 인접 리스트 표현
graph = [[] for _ in range(3)]
# 노드 0에 연결된 노드 정보 저장(노드, 거리)
graph[0].append((1, 7))
graph[0].append((2, 5))
# 노드 1에 연결된 노드 정보 저장
graph[1].append((0, 7))
# 노드 2에 연결된 노드 정보 저장
graph[2].append((0, 5))
print(graph)
📌두 방식의 차이
메모리 측면에서 인접 행력 방식은 모든 관계를 저장하므로 노드 개수가 많을수록 메모리가 불필요하게 낭비
인접 리스트 방식은 연결된 정보만을 저장하므로 메모리를 효율적으로 사용
속도 측면에서 인접 리스트 방식은 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느림
연결된 데이터를 하나씩 확인해야하기 때문
📌DFS 동작 과정
1. 탐색 시작 노드를 스택에 삽입하고 방문처리
2. 스택의 최상단 노드에 방문하지 않은 인접 노드 있으면 인접 노드를 스택에 넣고 방문처리
방문하지 않은 인접 노드가 더이상 없으면 스택에서 최상단 노드를 꺼냄
3. 2번의 과정을 더 이상 수행할 수 없을때까지 반복

def dfs(graph, v, visited):
# 현재 노드를 방문 처리
visited[v] = True
print(v, end=" ")
# 현재 노드와 연결된 다른 노드를 재귀적으로 방문
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
# 각 노드가 연결된 정보를 리스트 자료형으로 표현(2차원 리스트)
graph = [[], [2, 3, 8], [1, 7], [1, 4, 5], [3, 5], [3, 4], [7], [2, 6, 8], [1, 7]]
# 각 노드가 방문된 정보를 리스트 자료형으로 표현(1차원 리스트)
visited = [False] * 9
# 정의된 DFS 함수 호출
dfs(graph, 1, visited)
📌참고
이것이 취업을 위한 코딩 테스트다 with 파이썬
IT 취준생이라면 누구나 입사하고 싶은 카카오・삼성전자・네이버・라인!취업의 성공 열쇠는 알고리즘 인터뷰에 있다! IT 취준생이라면 누구나 가고 싶어 하는 카카오, 라인, 삼성전자의 2016년
www.google.com
'코딩테스트' 카테고리의 다른 글
| 음료수 얼려 먹기 (5) | 2024.10.13 |
|---|---|
| 탐색 알고리즘 BFS (4) | 2024.10.12 |
| 꼭 필요한 자료구조 기초 - 재귀함수 (3) | 2024.10.10 |
| 꼭 필요한 자료구조 기초 - 스택, 큐 (10) | 2024.10.08 |
| 게임 개발 (6) | 2024.10.07 |

